The selloff has abated somewhat here in Asia with only local markets falling on the back of both iron ore and coal concerns, as the USD remains firm against the risk currencies with gold still flummoxed at well below the $1800USD level:
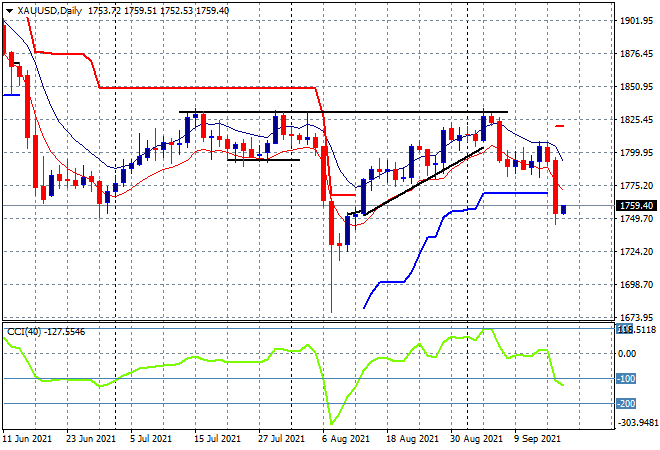
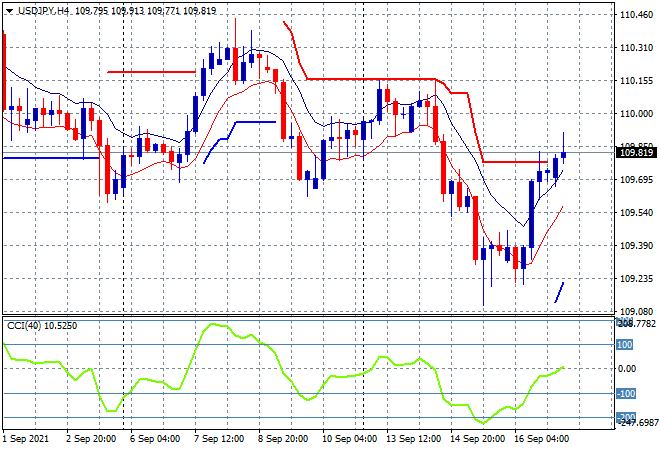
The Shanghai Composite is down 0.6% so far to remain below the 3600 point level while the Hang Seng Index has finally stopped falling with a minor bounce but is still below the 25000 point level, currently at 24765 points. Japanese stocks are also putting in some minor gains with the Nikkei 225 up 0.5% to 30484 points, helped by a much weaker Yen as the USDJPY pair tries to get back above the 110 handle after recently hitting a new weekly low:
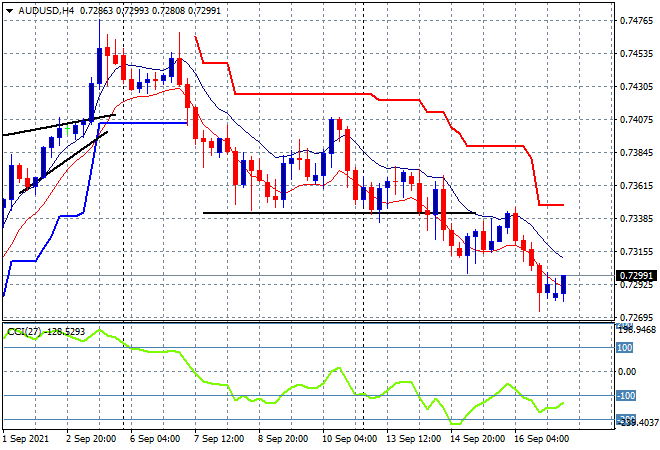
Australian stocks are the standout in the region by falling sharply, with the ASX200 about to close 1% lower at 7385 points as medium term support is wiped out while the Australian dollar was pushed through the 73 handle with momentum looking towards retesting the lows:
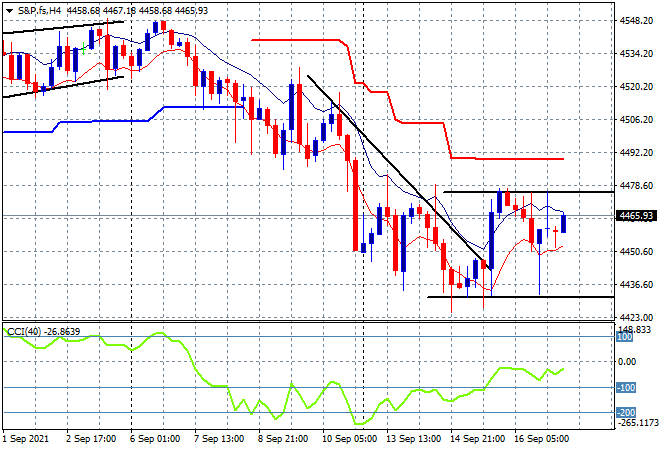
Eurostoxx and S&P futures are rising slightly heading into the London open with the four hourly chart of the S&P500 shows price tightly bound between the 4480 and 4440 point levels with momentum still not yet positive in the short term with the bears in charge – until the BTFD crowd steps in?
The economic calendar finishes the week with UK retail sales, Euro wide core inflation for August and then finishes up with the US Michigan consumer sentiment survey.