While we’re all fixated on the deglobalisation fireworks of Donald Trump and Pauline Hanson, neither is the most pressing threat. That honour still lies in Europe where French elections are again entering chaos as the conservative candidate, Francois Fillon, implodes, via The Independent:
French presidential hopeful and long-time front-runner François Fillon could be eliminated in the first round of the election, according to new polling, following allegations he paid close to €1m – most of it allegedly taxpayer-funded – to his wife and children as parliamentary aides with little evidence of work.
Less than three months before the vote, the right-wing candidate in the French elections is embroiled in a damaging scandal, which could yet dash his presidential hopes. Mr Fillon has denounced the allegations, saying that the work was genuine.
Conservative Mr Fillon has dropped below 20 per cent in the polls, paving the way for National Front (FN) candidate Marine Le Pen to extend her lead.
Far-right candidate Ms Le Pen is now leading the latest polls by Elabe and published in Les Echos with up to 27 per cent of voting intentions in the first round, which she is set to win. She is followed on 23 per cent by independent candidate Emmanuel Macron – who is expected to win the presidential race in a head-to head with Ms Le Pen in a second round.
Here are the latest poll results which do not look good for globalisation:

Thankfully Ms Le Pen still lagging Emmanuel Macron handsomely:
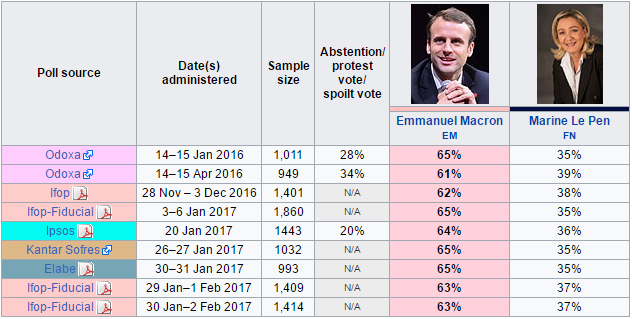
Mr Macron is a card-carrying europhile and open borders convert so the election shapes as a very clear pro and anti immigration vote.
That leaves Macron vulnerable if security circumstances deteriorate. Le Pen is probably wondering if Donald Trump has turned into a rather large liability.
Even so, with Macron so clearly in front it may provide some relief for the euro.

