Leonard Mlodinow’s terrific book The Drunkard’s Walk is an historical narrative on the philosophy of randomness and probability intertwined with modern statistical anecdotes. If the inner nerd in you enjoys a little mathematical philosophy like mine does it is definitely be worth the read.
The anecdotes in the book provide lessons on the cautious interpretation of statistics which are as relevant today as ever. This is especially the case given that econometrics, the statistical other half of economics, is often used in practice simply as an ‘economic trick’. In fact, I have my own criticisms of Mlodinow’s interpretation of the experimental outcomes that show people are poor at intuiting probability (which I cover below).
The final two chapters are by far the most interesting, covering human propensity to see patterns where there are none (including confirmation bias and the need to perceive control), how experts are routinely fooled by randomness, how success is often chance rather than the result of hard work, and how the butterfly effect was accidently discovered by Edward Lorenz in the 1960s (a random event itself).
An important lesson is found in Mlodinow’s analysis of the chances of a single fund manager’s success at beating the market for 15 consecutive years. It was simple down to chance.
Bill Miller was that fund manager. The probability that his long term success was simply down to luck was widely quoted as 1 in 372,529 (or 0.00026%). But this is the chance that if we had singled him out at the start of his 15 year streak, then followed his performance, and his only, for 15 years, that luck alone explained his success. But in reality this did not happen.
In fact this is a startling example of silent evidence. At the beginning of his 15 year ‘winning’ streak there were literally thousands of fund managers in the race to beat the market. It is only in retrospect that we praised Miller and forgot the rest. So the question then becomes what are the chances that one of these thousands of starters will beat the market for 15 consecutive years.
Since he was praised as the only fund manager in the past 40 years to beat the market for so long, Mlodinow then calculates that if 1000 fund managers (a huge underestimate) are in the race, that one of them will beat the market for a 15 year period by chance alone is around 75%. Conservatively, that means that it is 75% likely that Miller’s success was simply random chance, and only a 25% chance his skill contributed at all.
A second important lesson is the first law of probability: The probability that two events will both occur can never be greater than the probability that each will occur individually. While the law makes intuitive sense, the evidence presented that people fail to apply it to their reasoning is flimsy at best.
Mlodinow asks us to consider an experiment from Khaneman, Slovic and Tversky’s famous book on judgement under uncertainty. Given a brief description of Linda, 88 subjects were asked to rank the statements that follow on a scale of 1 to 8 according to their probability, with 1 representing the most probable, and 8 the least. The results are in the order ranked by the participants from most probable to least probable.
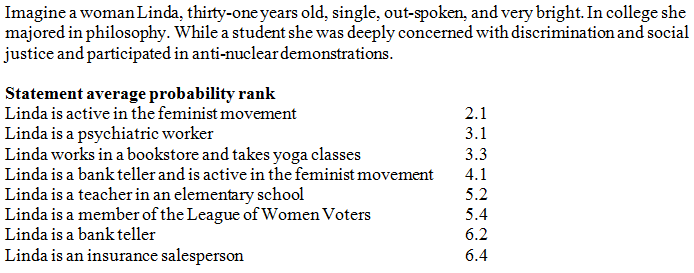 What stands out from this experiment is that the participants ranked the probability that Linda was a bank teller lower than the probability that she was a bank teller AND is active in the feminist movement. Since the bank teller statement captures the combined statement plus all options of being a bank teller and not active in the feminist movement, the probability should be higher.
What stands out from this experiment is that the participants ranked the probability that Linda was a bank teller lower than the probability that she was a bank teller AND is active in the feminist movement. Since the bank teller statement captures the combined statement plus all options of being a bank teller and not active in the feminist movement, the probability should be higher.
My reason for questioning whether people actually fail to intuit the true probability is that my personal interpretation was that the Linda is a bank teller statement implied that she wasn’t active in the feminist movement. By default my brain registered the separate itemisation of the option to mean that it did NOT capture the bank teller and feminist statement.
In fact the respondents may have been completely correct if we apply the NOT criteria to the bank teller choice. The diagram below shows the nested probabilities we could apply to the question. The chances of being a banker and feminist are 40%, while simply being a banker is 50%. When we change our interpretation of the statement, the probability of being a banker and not a feminist are just 10%.
 After all, the logical survey participant might rightly question the inclusion of just one of the statements having two qualifying criteria, and imply that the reverse is true for the other statement. I did.
After all, the logical survey participant might rightly question the inclusion of just one of the statements having two qualifying criteria, and imply that the reverse is true for the other statement. I did.
So, depending on how we define the criteria, and how we perceive the problem, the probability changes. My personal view is that people instinctively may be better at understanding probability than believed by Khaneman et al., and reiterated by Mlodinow.
To me, a far better example of how people fail to intuit probability is weather variation. A weather event observed 10 times in a century becomes a 1 in 10 year event, which people then expect to happen with almost certainty every ten years. In reality however, the chance that the 1 in 10 year event will occur in any 10 year period is closer to 65%, and for a twenty year period the chance of having a 1 in 10 year event is still only 87%.
What is the real lesson? Don’t forget to bring logic and commonsense to statistics and economic tricks.
Tips, suggestions, comments and requests to [email protected] + follow me on Twitter @rumplestatskin