It has been quite some time since I did a post in the Macro 101 thread. There has simply been too much economic news to process lately. However, now that the stock markets seemed to have stabilised themselves at a lower base, and the western world has set itself up for a recession I think I have a spare few hours to revisit this thread.
Previously I have discussed banking credit, foreign trade and sectoral balance. Today I am going to try to unify these things through a conversation about reserves and interest rates.
So before I start I need you to ask yourself two questions.
- What does the term “reserve” actually mean in the title “Reserve bank of Australia” ?
- How exactly does the RBA control interest rates.?
If you know the answer to these questions then maybe you don’t need to read on. Otherwise let’s dive in.
I will be working through transactions step-by-step in order to slowly add complexity. I will obviously be over simplifying examples, and in some cases change the order of how things that actually occur in in order to explain things more simply. But none of these things change the actual functions/tasks that are occurring, it just makes it easier for me to explain the process.
In a previous post on banking credit I talked about “money of account” and “money of exchange”. If you get stuck with these concepts while reading this post please go back and read the previous post for more detail.
From the beginning then…
You decide to purchase a car from a dealer for $40,000, the dealer banks with CBA, you bank with ANZ. You approach ANZ for a loan and given your wonderful credit rating you are approved. The steps of the transfer are as follows:
- The ANZ creates a new loan record and assigns it an outstanding balance of $40,000 under your name.
- At the same time it adds $40,000 to your account.
So far this entire transaction is internal to the bank. This is simply a change in the database that the bank uses to store account information. So although you think you have an additional $40,000 nothing has really happened apart from a few electrons have been re-aligned on a hard drive(s) somewhere inside the ANZ’s data-centre. This is “money of account”.
So next you want to pay the car dealer who banks at CBA. To do this you could use a bank cheque, personal cheque, cash, money order etc. It really doesn’t matter how what the medium of transfer is. However what you will note is that the electrons that were re-arranged on ANZs hard-disk(s) have no value to the CBA. So how exactly does ANZ transfer $40,000 to CBA in order to satisfy the transaction? Enter “money of exchange” otherwise known as “reserves” which are recorded on the reserve bank’s computer.
Banks transfer reserves to and from each other via their reserve banks accounts. In Australia they are called Exchange Settlement Accounts and you can read about them here.
In future examples I will refer to these as “reserve accounts” for simplicity but it must be noted that in fact an ESA is a special type of reserve account that is only available to banks that have access to the interbank lending markets. There are other reserve accounts that are used by foreign central banks to record their AU$ reserves.
Now let’s describe the transaction that occurs for you to purchase that car.
- You give the car dealer a cheque for your car.
- The dealer takes the cheque to CBA and deposits it in his/her business account.
- CBA processes the cheque and demands $40,000 of reserves from ANZ
- At the ANZ the balance of your account is deducted by $40,000 and requests the RBA move $40,000 from its reserve account to CBA’s reserve account.
- At the CBA the car dealers account is adjusted by $40,000
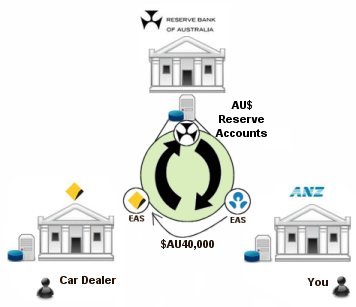
So now we have 3 sets of electrons being re-aligned. Firstly at ANZ the account database is once again updated to record that your account has lost $40,000. The database at the reserve bank is updated to record that $40,000 of reserves was deducted from ANZ’s exchange settlement account and added to CBA’s exchange settlement account. Finally at the CBA, their database is updated to show that your car dealer has an extra $40,000.
Functionally the same process occurs if you used cash. Because a $5 note is simply a plastic/paper version of a $5 reserve balance and are completely interchangeable.
Now obviously you are not the only one doing a banking transaction that day, there are in fact tens of millions of inter-bank transactions each day in Australia. Each one affects the account balance in each bank’s reserve account. Over the period of the each day the balances of these accounts will fluctuate but the RBA specifies that these accounts must have a positive balance at all times ( more on that point later ).
The important thing to understand is that the amount of reserves required is much smaller than the total of the bank’s “money of account”. For example, if on the same day your loan and cheque were processed, a $40,000 loan was issued by CBA and a subsequent cheque given to an ANZ customer then technically there would be no change in either banks reserve accounts even though both banks issued $40,000 loans.
But in reality that is not normally the case. When a bank runs a loan book it requires reserves in order to support interbank transfers and over the counter transactions because of the demand for the “money of account” that those loans created when they were issued.
So as a bank issues loans it must seek reserves to support its liquidity requirements due to those loans. So there will obviously come a point when a bank simply does not have enough reserves to support additional loans. The bank therefore has two choices; stop issuing more credit until some existing loans are repaid, that is some reserves are returned to the bank, or borrow reserves from someone else.
Obviously banks want to continue to grow their loan book because loans are profitable, so 99.99% of the time banks seek additional reserves.
But where from? I have previously heard some people state that banks can just issue a loan to themselves and use the created deposit to fund further lending. But if you have been reading carefully you will understand that this just creates more “money of account” in their accounts database in their own computer. It certainly doesn’t add to the balance of their reserve account in the reserve banks computer or suddenly create a pallet of $100 notes (remember cash and reserve balances are interchangeable). So in fact this would not help at all.
Banks can only get more reserves from two places, other entities that have an ESA or from the reserve bank itself. Now I can hear what you are saying already. You are saying “hang on DE, Australian banks get most of their funding from overseas through bond issuance”. Yes they do! However you need to understand exactly what this means in terms of reserves to appreciate that both statements hold true. So let explain.
As I have been saying the RBA is a bank for banks. It is where they store and borrow Australian dollar reserves. That is why it is called the “Reserve bank of Australia”. (Question 1 above ). All across the globe there are similar institutions for each unique currency. The US has the Fed which records US reserves, China has the PBoC which records Yuan reserves, the EU has the ECB which records Euro reserves, and so on. At each of these institutions, foreign central banks also have non-EAS reserve accounts. These accounts are used to support international exchange and trade.
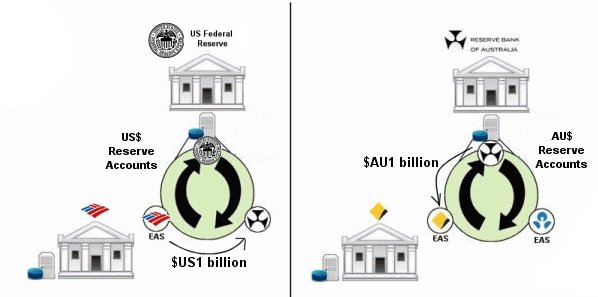
So let’s look at what happens when the CBA issues AU$1 billion 5-year bonds and a US superannuation fund purchases them. We will assume that the fund already has $AU1 billion equivalent of US$ in a US savings account at the Bank of America, and that the exchange rate is 1.00. Again this has all been oversimplified.
- The fund agrees to buy the bonds and instructs the Bank of America to pay the CBA $1billion Australian dollars.
- At the bank of America the balance of the savings account in their computer in the name of the superannuation fund is lowered by $US 1 billion.
- The Bank of America then transfer $US 1billion dollars of its reserves to the Reserve Bank of Australia’s US reserve account (non-ESA) under an order to issue the equivalent amount (governed by the exchange rate) of AU$ to the CBA.
- At the same time the Reserve bank of Australia adds $AU 1billion to the reserve account of the CBA in its computer.
So let us recap. $US1 billion of “money of account” was subtracted from an superannuation funds’ account in the database of the Bank of America, $US1billion of reserves was transferred from the reserve account of the Bank of America to the reserve account of the RBA in the database of the US Federal reserve, and finally, $AU1 billion was added to the balance of the Exchange Settlement Account of CBA in the database at the RBA. The CBA now has another $1 billion dollars worth of loan liquidity supporting reserves, and the RBA has gained $1US billion dollar of US reserves.
As you can see from that example the CBA actually got its reserve from the RBA because it is in fact the only place that could issue them. This is because reserves are simply electronic records in the RBA’s computer, which is why no one else can issue them. This may sound like a trivial statement, but it is in fact the basis on which modern economies are built.
Moving on… Obviously over time the CBA must pay interest on those bonds, which will move a proportion of those reserves back in the opposite direction, but by this time the loans that these bonds support will have matured somewhat so new reserves will exist to make those payments. At the time of bond maturity the entire process will be reversed meaning that $AU1 billion worth of reserves would be removed from the bank’s ESA. You may now appreciate why banks must continually rollover funding and are therefore constantly susceptible to liquidity risk.
There is however a fairly large problem with the fact that a bank suddenly receives $AU1 billion dollars in reserves because it has suddenly flooded the interbank market with reserves. This would tend to drive down interbank interest rates which would undermine the RBA’s interest rate.
This leads nicely into a discussion about the interbank lending market and how the RBA controls interest rates through it. I was going to actually write about this myself, however it turns out that the RBA has a very good document available explaining it all for me. The one issue with that document is that it required you to have some background knowledge of reserves and exchange settlement accounts before you read it. I hope I have done a fair job of explaining these concepts to you. If that is the case then you hopefully will not struggle too much with the following document.
Good luck.